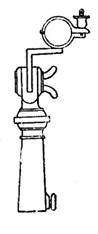
Moller device

The device, designed by Colonel (later General) G. L. Moller, commander of the Vilna artillery firing range, and tested for a long time at the Officers’ Artillery School in Tsarskoe Selo, was not officially adopted by the Russian Army, but it was used by the Bulgarian fortress-siege artillery between the end of the 19th and the beginning of the 20th century.
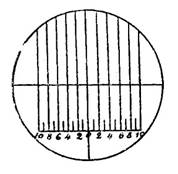
The device consisted of two separate binoculars, which could be used separately, or together, as a common instrument. Both binoculars have the same device. On one of the lenses of the eyepiece tube of both binoculars was engraved a horizontal scale of divisions composed of 5 long vertical lines and 5 short vertical lines to the left and the same number to the right, relative to a long vertical line passing through the centre. The long central line was marked with 0, while the long lines to the left and right with the numbers 2, 4, 6, etc. Another unnumbered long line was engraved in the middle of the lens perpendicular to the above lines. The lenses of the other eyepiece tubes were transparent and without graduations; they served only to help one see the observed object more clearly.
The size of the engraved divisions was such that the angular unit of a division (between a short line and a long line) corresponded to 6’, that is, the angle formed by joining the edges of a division to the centre of the eyepiece was equal to 6’ minutes. The distance between the extreme divisions was 2°. The two binoculars were placed on a tripod stand, which allows them to be rotated horizontally and vertically. Use of the Moller device The Moller device could be used : a) to determine the lateral deflection of the projectile, using the binoculars separately. The binoculars, placed on the tripod support firmly planted in the ground, were positioned in plain sight and in a horizontal position, so that the scale marks occupied a vertical position. By acting on the tripod screws, the long vertical line marked with 0 was directed towards the objective, and the other unnumbered line, which in that position had a horizontal direction, was also referred to that point. During the shot, the observer only had to see against which division of the scale the projectile had burst to determine with a simple formula how many meters the projectile on the left or right deflected from the point where the observation was carried out. Knowing that the circle arch that underlies an angle of 1’ is equal to 0.0003 of the radius with which the arch is described and that the arch corresponding to a division of the device (6’) is 6 times greater, since the length D is the extent of the processes of the projectile included in a division, and R is the distance from the target, it is easy to determine D when knowing R. For example, if the distance from the target is 2200 m, the value of a division of the device is D = 0.0003 x 2200 x 6 = 3.96 = 4 m, when the projectile is seen below 5 divisions, its derivation in meters is 4 x 5 = 20 m. b) To determine the height of the dispersion of the shrapnel, using both binoculars together. In this case, the observer proceeded as above, with the difference, that the binoculars were placed one under the other, so the marks of the scale were horizontal and the long numbered line with 0 was directed to the line or to the point with respect to which the height of dispersions is calculated. c) To determine the width of the target, if the distance from it is known, or vice versa, and to determine the depth of the target, if the distance from it is known, using the binoculars separately. The observer determines how many tools of the device cover the target, for example 4 divisions. For the first case, we have: D = 0.0003 R d or R = D/0.0003 d, where d indicates the divisions of the device in which the target is enclosed, expressed in minutes. So, if the target width is 40 m, R = 40/0.0003 x 24 = 5.555 m. For the second case, if the distance is known and equal to 5.555 m, we have: D = 0.0003 R d or D = 0.0003 x 5.555 x 24 = 40 m. d) To determine the deflection of the projectile in the distance, placing the two binoculars one on the right and the other on the left of the battery. When shooting great distances, the base (the distance between the two tripods) should not be less than 200 m. The two binoculars were aimed so that the long lines numbered 0 on the scale, taking a vertical position, point to the same point on the target, using an auxiliary point. When the shot is fired, the two observers noted against which division of the scale the projectile had fallen and whether it was to the left or right of the line numbered with 0. If an observer noticed the dispersion of the projectile on the side of the zero line, from which his own battery was located (for the observer on the right from the left and for the one on the left from the right), he reported the number of divisions under which he had observed the fall, with the sign –, if he had noticed it on the opposite side, he reported it with the sign +. The algebraic sum of the data from the two devices gave the numerical value of the long or short projectile burst. For example, if one observer gives a reading of –4 and the other +7, their algebraic sum is –4 +7 = +3, indicating that the projectile is falling behind the target. Knowing this data (+3) and the value of one division of the device in meters for the given position, through a conversion formula the observers could determine how many meters the projectile had fallen behind the target. The value of a division of the device should also be determined in minutes of the elevation angle or in graduations of the sight, to establish by how much the elevation of the gun had to be increased, to move the trajectory forward or backward according with the determined value in meters of a division of the device. These values could be determined in advance by calculation, or obtained directly from the results of the first two shots. In this second case, after each of the two shots, the observers noted the readings of their devices (algebraic sum) : the difference in the sight heights or in the elevation angle for the first and second shots divided by the numerical (arithmetic) sum of the readings of the devices for these two shots gives the value of a division, in sight graduation or in minutes, from which the corresponding value in meters is easily obtained. For example, shooting with a 15cm L/30 cannon at a distance of 3900 m, the indications of the devices gives : –4 for a sight height of 110 graduations, +8 for a sight height of 118 graduations. Knowing that at this distance a sight graduation varies the distance by 24 m, with a difference in the elevation heights of 8 graduations, we obtain: 8x24=192 m. Since the sum of the readings of the devices is 8+4=12, each unit of the readings of the devices corresponds to 192/12 = 16 m. e) To determine the interval of dispersion of the shrapnel bursts, the observer proceed as above.
SOURCES : - Ръководство за занятията въкреспостата артилерия. Част IV. Подготовка и служба на наблюдателите, Sofia 1902, pp. 26-32; - FRAENKEL. J. : “Cours pratique de tir à l’École des officiers de l’artillerie russe en 1884 et 1885” : Revue d’Artillerie XXIX (Octobre 1886 – Mars 1887), pp. 264-265.